前回、三角関数の有理関数を積分するために変数変換した時に思いがけない障害が生じた。今回はパラメータ表示に立ち返って考察する。
三角関数のパラメータ表示
三角関数のパラメータ表示については 抽象数学の手ざわり(斎藤毅) が参考になった。単位円 \( C:x^2+y^2=1 \) を考える。\(C\) 上の点 \( (-1,0) \) を通る傾き \(t\) の直線 \( y=t(x+1) \) と \(C\) のもう1つの交点を求めると、\( \left( \frac{1-t^2}{1+t^2},\frac{2t}{1+t^2} \right) \) が得られる。\(C\) 上の点なので、\( (\cos\theta,\sin\theta) \) と書ける。右図を参照すれば、傾きは \( \tan \frac{\theta}{2} \) と分かる。以上をまとめて変数変換で使われた式が得られる。
\( \tan \frac{\theta}{2} = t,\, \cos \theta = \frac{1-t^2}{1+t^2},\, \sin \theta = \frac{2t}{1+t^2} \)
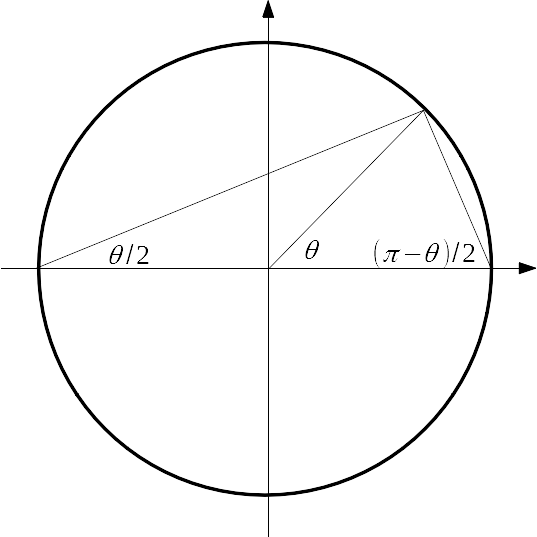
この変数変換で問題となったのは \( \theta=\pi \) の時であった。 それは対応する点 \((-1,0)\) が \(t\) を使って表現できないことに起因する。別の点を基準にすれば、その点で問題が生じるかもしれないが、 \( (-1,0) \) での問題は解決できると期待される。\((1,0)\) を通る傾き \(s\) の直線 \( y=s(x-1) \) を使って同じ議論をしてみよう。交点を求めると、\( \left(\frac{s^2-1}{s^2+1},\frac{-2s}{s^2+1}\right) \) となる。図より直線の傾きは \( s = -\tan \frac{\pi-\theta}{2} = \tan \frac{\theta-\pi}{2} = – \cot \frac{\theta}{2} \) となる。以上をまとめると、次のパラメータ表示になる。
\( \begin{eqnarray}
&& \cot \frac{\theta}{2} = -s \\
&& \cos \theta = \frac{s^2-1}{s^2+1} \\
&& \sin \theta = \frac{-2s}{s^2+1} \\
\end{eqnarray} \)
代わりに \( \cot \frac{\theta}{2} = t,\, \cos \theta = \frac{t^2-1}{t^2+1},\, \sin \theta = \frac{2t}{t^2+1} \) とすることもできる。その場合は、\( \theta \) が増加すると \(t\) は減少する。
通常使われる変数変換では \( (-1,0) \) が除かれるので、\( \theta=(2n+1)\pi \) では不都合が生じる。今回の変数変換では \( (1,0) \) が除かれるので、\( \theta=2n\pi \) で不都合が生じる。
積分への応用
実際の積分に応用してみよう。\( \displaystyle \int\frac{3}{5+4\cos \theta} \,d\theta \) を求める。\( \cot \frac{\theta}{2} = -s \) とおくと、\( \displaystyle \frac{d\theta}{2\sin^2\frac{\theta}{2}} = \frac{(s^2+1)d\theta}{2} = -ds \) だから、\( \displaystyle d\theta = \frac{-2ds}{s^2+1} \) となる。
\( \begin{eqnarray}
\int\frac{3}{5+4\cos \theta} \,d\theta
&=& \int\frac{3}{5+\frac{4\left(s^2-1\right)}{s^2+1}} \,\frac{-2ds}{s^2+1} \\
&=& \int\frac{-6ds}{9s^2+1} \\
&=& -2 \arctan 3s + C \\
&=& -2 \arctan \left( 3\cot \frac{\theta}{2} \right) + C \\
\end{eqnarray} \)
区間 \( [\frac{\pi}{2},\frac{3}{2}\pi] \) における定積分を求めよう。積分区間に \( \theta = 2n\pi \) が含まれていないので、不定積分の結果がそのまま利用できる。
\( \begin{eqnarray}
\int_{\frac{\pi}{2}}^{\frac{3}{2}\pi} \frac{3}{5+4\cos \theta} \,d\theta
&=& \left[ -2 \arctan \left( 3\cot \frac{\theta}{2} \right) \right]_{\frac{\pi}{2}}^{\frac{3}{2}\pi} \\
&=& 4 \log 3 \\
\end{eqnarray} \)
まとめ
三角関数の有理関数の積分は変数変換で有理関数に変換するのが定跡手順である。一般に紹介されている変換では、\( \theta=(2n+1)\pi \) で不都合が生じることを前回の記事で実例をもって示した。今回の記事では別のパラメータを与えて、不都合な点が \( \theta=2n\pi \) に移動した。積分区間によ応じて適切な変数変換を利用すれば良いということになる。大げさに言えば、円を多様体として見て、局所座標系を導入したとも言える。円を繰り返し回ることはできるので、螺旋に近いのかもしれない。
