余接関数の部分分数展開

\( \cot z \) を例に部分分数展開の方法を学ぶ。主に 複素関数入門(神保道夫) を参照した。

\( \pi \cot \pi z\) の部分分数展開

極が整数、留数が 1 になるように \( f(z) = \pi \cot \pi z\) としておく。同じ極をもつ関数として \( \displaystyle \sum_{n=-\infty}^{\infty} \frac{1}{z-n} \) が考えられるが、収束性について注意が必要である。\(\pm\infty\) への両方に極限をとっているが、独立に行うと収束しない。例えば、\( \displaystyle \sum_{n=1}^\infty \frac{1}{z-n} \) は存在しない。実際、\( z=\frac{1}{2} \) を代入すると、

\( \displaystyle \sum_{n=1}^\infty \frac{2}{1-2n} = -2 \sum_{n=1}^\infty \frac{1}{2n-1} < -2 \sum_{n=1}^\infty \frac{1}{2n} = – \infty \)

となる。そこで

\( \displaystyle \frac{1}{z}+\sum_{n=1}^{\infty} \left( \frac{1}{z-n} + \frac{1}{z+n} \right) = \frac{1}{z}+\sum_{n=1}^{\infty} \frac{2z}{z^2-n^2} \)

とすれば収束することを示す。十分大きな \(N\) に対して、\(n>N\) ならば \(\displaystyle \left|z^2-n^2\right| \geq n^2 -\left|z\right|^2 > \frac{1}{2}n^2 \) だから、\( \displaystyle \sum_{n>N} \frac{1}{\left| z^2-n^2 \right| } \leq 2 \, \zeta(2) \) となり、絶対収束する。この後、\( \pi\cot \pi z \) の部分分数展開

\( \begin{eqnarray}
f(z) &=& \frac{1}{z}+\sum_{n=1}^{\infty} \frac{2z}{z^2-n^2}
\end{eqnarray} \)

を示す。

証明の方針

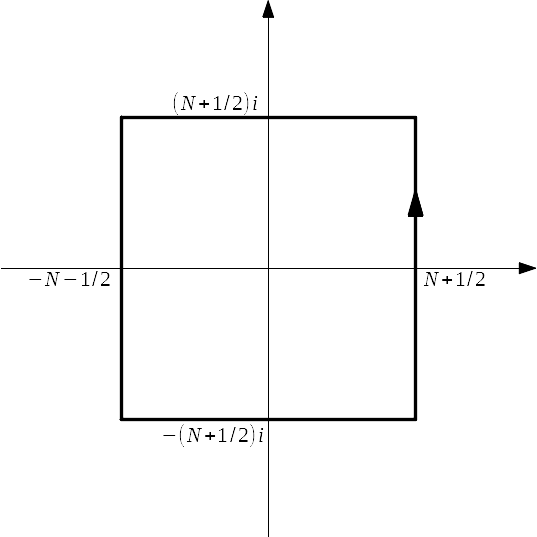
留数による計算

\( \displaystyle \frac{f(\zeta)}{\zeta-z} \) は１位の極として \( \zeta = -N,\,-N+1,\,\cdots,\,N-1,\,N \) の他に \( \zeta=z \) をもつから、留数定理により次の式が成り立つ。

\( \begin{eqnarray}
\frac{1}{2\pi i}\int_{C_N}\frac{f(\zeta)}{\zeta-z}\,d\zeta
&=& \mathop{\rm Res}\limits_{\zeta=z} \frac{f(\zeta)}{\zeta-z} + \sum_{n=-N}^N \mathop{\rm Res}\limits_{\zeta=n} \frac{f(\zeta)}{\zeta-z} \\
&=& f(z) + \sum_{n=-N}^N \mathop{\rm Res}\limits_{\zeta=n} \frac{f(\zeta)}{\zeta\,-\,z}
\end{eqnarray} \)

和の中の留数を求めよう。

\( \begin{eqnarray}
\mathop{\rm Res}\limits_{\zeta\rightarrow n} \frac{f(\zeta)}{\zeta\,-\,z}
&=& \lim_{\zeta\rightarrow n} (\zeta \,-\, n) \cdot \frac{f(\zeta)}{\zeta\,-\,z} \\[1mm]
&=& \lim_{\zeta\rightarrow n} \frac{\pi( \zeta \,-\, n )}{\sin \pi \zeta} \cdot \frac{\cos \pi \zeta}{\zeta\,-\,z} \\[1mm]
&=& (-1)^n \cdot \frac{(-1)^n}{n\,-\,z} \,=\, \frac{1}{n\,-\,z}
\end{eqnarray} \)

したがって、留数による計算は次のようになる。

\( \begin{eqnarray}
\frac{1}{2\pi i}\int_{C_N} \frac{f(\zeta)}{\zeta-z}\,d\zeta
&=& f(z) \,-\, \sum_{n=-N}^N \frac{1}{z\,-\,n} \\
&=& f(z) \,-\, \frac{1}{z} \,-\, \sum_{n=1}^N \left( \frac{1}{z\,-\,n} + \frac{1}{z\,+\,n}\right) \\
&=& f(z) \,-\, \frac{1}{z} \,-\, \sum_{n=1}^N \frac{2z}{z^2\,-\,n^2} \\
\end{eqnarray} \)

後は、\( N\rightarrow \infty \) として左辺が 0 になれば証明は完了する。

積分経路に沿った計算

\( \displaystyle \int_{C_N}\frac{f(\zeta)}{\zeta-z}\,d\zeta \rightarrow 0 \) を示す。\( \displaystyle \left| \int_{C_N}\frac{f(\zeta)}{\zeta-z}\,d\zeta \right| \leq \int_{C_N} \left| \frac{f(\zeta)}{\zeta-z} \right| \,\left| d\zeta \right| \) として、右辺が 0 に収束することを示すのが定跡手順であるが、実はこのままでは困難が生じる。積分経路の長さは \(N\) に比例して大きくなるので、被積分関数が \( \frac{1}{N} \) より速く 0 に収束して欲しいが、周期性 \( f(\zeta+n\pi)=f(\zeta) \) から \( f(\zeta) \) は定数オーダー、\( \frac{1}{\zeta \,-\, z } \) はオーダー \(\frac{1}{N}\) であり、期待通りにはならないようだ。巧妙な変形

\( \displaystyle
\frac{f(\zeta)}{\zeta-z}
= \frac{(\zeta-z+z)f(\zeta)}{\zeta(\zeta-z)}
= \frac{f(\zeta)}{\zeta}
+\frac{f(\zeta)}{\zeta(\zeta-z)}
\)

を行うと、最後の式の第２項は目的にかないそうだ。そこで、\( \displaystyle \left| \int_{C_N}\frac{f(\zeta)}{\zeta-z}\,d\zeta \right| \leq \left| \int_{C_N} \frac{f(\zeta)}{\zeta} \, d\zeta \right| + \left|\int_{C_N} \frac{f(\zeta)}{\zeta(\zeta-z)} \, d\zeta \right| \) としてから右辺の２つの積分を独立に処理しよう。

\( \frac{f(\zeta)}{\zeta} \) に関する積分は「複素関数入門」では偶関数であることから 0 としているが、ここでは留数定理で求めよう。

\( \displaystyle
\frac{1}{2\pi i}\int_{C_N}\frac{f(\zeta)}{\zeta}\,d\zeta
= \sum_{n=-N}^N \mathop{\rm Res}\limits_{\zeta=n} \frac{f(\zeta)}{\zeta}
\)

\( \zeta = 0 \) が２位の極になっているので \( \zeta\neq 0 \) の場合とは別に求めよう。\( f(\zeta) = \frac{1}{\zeta} + c_0 + c_1 \zeta + \cdots \) の定数項を求めればよい。\(c_0\) は \( f(\zeta) \,-\, \frac{1}{\zeta} \) に対して \( \zeta\rightarrow 0 \) とすれば求まる。

\( \begin{eqnarray}
\frac{f(\zeta)}{\zeta} – \frac{1}{\zeta}
&=& \frac{\pi \zeta \cos \pi\zeta \,-\, \sin \pi\zeta }{\zeta \sin \pi\zeta} \\[1mm]
&=& \frac{\pi\zeta}{\sin \pi\zeta} \cdot \frac{\pi \zeta \cos \pi\zeta \,-\, \sin \pi\zeta }{\pi \zeta^2} \\[1mm]
&=& \frac{\pi\zeta}{\sin \pi\zeta} \cdot \frac{1}{\pi \zeta^2} \cdot \left( \pi \zeta \left( 1 – \frac{\pi^2}{2} \zeta^2 + \cdots \right) \,-\, \left( \pi\zeta \,-\, \frac{\pi^3}{6} \zeta^3 + \cdots \right) \right) \\[1mm]
&=& \frac{\pi\zeta}{\sin \pi\zeta} \cdot \left( -\frac{\pi^2}{3}\zeta + \cdots \right) \\[1mm]
&\rightarrow& 0 \quad(\zeta\rightarrow 0)
\end{eqnarray} \)

したがって、 \( \displaystyle \mathop{\rm Res}\limits_{\zeta=0} \frac{f(\zeta)}{\zeta} = 0 \) である。続いて \( \zeta=n\neq 0 \) の留数を求めよう。

\( \begin{eqnarray}
\mathop{\rm Res}\limits_{\zeta=n} \frac{f(\zeta)}{\zeta}
&=& \lim_{\zeta\rightarrow n} \frac{(\zeta \,-\, n ) f(\zeta)}{\zeta} \\
&=& \lim_{\zeta\rightarrow n} \frac{\pi(\zeta \,-\, n )}{\sin \pi \zeta } \cdot \frac{\cos \pi \zeta}{\zeta} \\[1mm]
&=& \frac{1}{n} \\
\end{eqnarray} \)

\( \displaystyle \mathop{\rm Res}\limits_{\zeta=n} \frac{f(\zeta)}{\zeta} +\mathop{\rm Res}\limits_{\zeta=-n} \frac{f(\zeta)}{\zeta} = \frac{1}{n}+\frac{1}{-n} = 0 \) なので \( \displaystyle \int_{C_N}\frac{f(\zeta)}{\zeta}\,d\zeta = 0 \) となり、１つ目の積分が解決した。

\( \frac{f(\zeta)}{\zeta(\zeta-z)} \) に関する積分は経路に沿って評価する。\( N > 2|z|\) ならば \( |\zeta (\zeta \,-\, z)| > \frac{1}{2}N^2 \) が成り立つ。\( \zeta=\alpha + i\beta \) とおく。積分路 \( \displaystyle C_N \) を４辺に分割し、各辺の上で積分値を評価する。\( L \) を積分路の上辺または下辺とすると、 \( |\alpha|\leq N+\frac{1}{2},\,|\beta|= N+\frac{1}{2} \) となる。

\( \begin{eqnarray}
\left| \cot \pi z \right|
&=& \frac{\left| e^{2\pi i \zeta} + 1 \right|}{\left| e^{2\pi i \zeta} \,-\, 1 \right|} \\[1mm]
&=& \frac{\left| e^{- 2\pi \beta + 2\pi i \alpha } + 1 \right|}{\left| e^{- 2\pi \beta + 2\pi i \alpha } \,-\, 1 \right|}
= \frac{\left| 1 + e^{2\pi \beta \,-\, 2\pi i \alpha } \right|}{ \left| 1 \,-\, e^{ 2\pi \beta \,-\, 2\pi i \alpha } \right|}\\[1mm]
&\leq& \frac{ 1+e^{- 2\pi |\beta| } }{1\,-\,e^{- 2\pi |\beta| } }
= \frac{ 1+e^{- (2N+1) \pi } }{1\,-\,e^{- (2N+1) \pi } }\\
\end{eqnarray} \)

最後の式は \( N \rightarrow \infty \) とすると 1 に収束するから、十分大きい \(N\) に対して \( \left| \cot \pi z \right| < 2 \) となる。

\( \begin{eqnarray}
\left| \int_L \frac{f(\zeta)}{\zeta(\zeta-z)}\,d\zeta \right|
&\leq& \left( 2N+1 \right) \cdot \frac{2\pi}{\frac{1}{2}N^2} \\[1mm]
&\rightarrow& 0 \quad (N\rightarrow \infty)
\end{eqnarray} \)

よって、上辺、下辺での積分値は 0 に収束する。\(L\) を右辺、左辺とすると、\( |\alpha|= N+\frac{1}{2},\,|\beta|\leq N+\frac{1}{2} \) となる。このとき、\( e^{2\pi i \alpha}=-1 \) である。

\( \begin{eqnarray}
\left| \cot \pi z \right|
&=& \frac{\left| – \, e^{- 2\pi \beta } + 1 \right|}{\left| – \, e^{- 2\pi \beta } \,-\, 1 \right|} \\[1mm]
&=& \frac{\left| 1 \,-\, \, e^{- 2\pi \beta } \right|}{\left| 1 + e^{- 2\pi \beta } \right|} = \frac{\left| 1 \,-\, \, e^{2\pi \beta } \right|}{\left| 1 + e^{2\pi \beta } \right|}\\[1mm]
&\leq& \frac{1 \,-\, e^{ – \, 2\pi |\beta| } }{ 1 + e^{ – \, 2\pi |\beta| } } < 1
\end{eqnarray} \)

\(L\) 上の積分値を評価する。

\( \begin{eqnarray}
\left| \int_L \frac{f(\zeta)}{\zeta(\zeta-z)}\,d\zeta \right|
&\leq& \left( 2N+1 \right) \cdot \frac{\pi}{\frac{1}{2}N^2} \rightarrow 0 \quad (N\rightarrow \infty)
\end{eqnarray} \)

以上により、\( \displaystyle \int_{C_N} \frac{f(\zeta)}{\zeta-z}\,d\zeta \rightarrow 0\quad(N\rightarrow \infty) \) が示された。