相補公式
「相補公式」はガンマ関数の次の関数等式で「相反公式」とも呼ばれる。
\( \begin{eqnarray}
\Gamma(z) \, \Gamma(1-z) &=& \frac{\pi}{\sin \pi z}
\end{eqnarray} \)
両辺ともに極の様子が確認しやすい。\( \Gamma(z) \) は負でない整数で1位の極であり、\( \Gamma(1-z) \) は正の整数で1位の極なので、左辺全体ではすべての整数で1位の極である。\( \sin \pi z \) は整数で1位の零点となっているから、右辺もすべての整数で1位の極である。また、\( z=\frac{1}{2} \) を代入すると、左辺は \( \Gamma\left( \frac{1}{2} \right)^2=\pi \) であり、右辺も \( \pi \) であることは容易に分かる。
証明
\( 0 < z < 1 \) と仮定して、複素関数論の助けを借りて証明する。微積分だけによる証明は 解析入門 I (杉浦光夫) またはその元になった ガンマ関数入門(E.アルティン) に紹介されている。一致の定理により一般の \(z\) に拡張できる。ベータ関数とガンマ関数の関係式により、
\( \begin{eqnarray} \Gamma(z) \, \Gamma(1-z) &=& B(z,1-z) \\
&=& \int_0^1 t^{z-1} (1-t)^{-z} \,dt\\
&=& \int_0^1 \frac{1}{t} \left( \frac{1}{t}-1 \right)^{-z} \,dt\\
\end{eqnarray} \)
である。\(\displaystyle u=\frac{1}{t} \,-\, 1 \) とおくと、次式が得られる。
\( \begin{eqnarray}
\Gamma(z) \, \Gamma(1-z)
&=& \int_0^\infty \frac{u^{-z}}{1+u} \, du \tag{#}\\
\end{eqnarray} \)
右辺が \( \displaystyle \frac{\pi}{\sin \pi z} \) であることを示せば証明は完了する。積分を求める前に、関数論講義(金子晃) にベータ関数を経由せずに等式 (#) を導く方法があるので記載しておこう。
\( \begin{eqnarray}
\Gamma(z) \, \Gamma(1-z)
&=& \int_0^\infty e^{-s}s^{z-1} \, ds \, \int_0^\infty e^{-t} t^{-z} \, dt \\
&=& \iint_{s\geq 0,\, t\geq 0} e^{-s-t}s^{z-1} t^{-z} \, dsdt \\
\end{eqnarray} \)
\( t=su \) として、\( s,\,u \) の積分に書き換えると、\( s \geq 0,\, u \geq 0 \), \( \displaystyle dsdt =\left| \mathrm{det} \left( \begin{array}{cc} 1 & 0 \\ u & s \end{array} \right) \right| \, dsdu = s \, dsdu\) だから次のようになる。
\( \begin{eqnarray}
\Gamma(z) \, \Gamma(1-z)
&=& \iint_{s\geq 0,\, u\geq 0} e^{-s-su} u^{-z} \, dsdu \\
&=& \int_0^\infty u^{-z} \left( \int_0^\infty e^{-(1+u)s} \,ds \right) \,du \\
&=& \int_0^\infty \frac{u^{-z}}{1+u} \,du \\
\end{eqnarray} \)
積分の計算
\( \displaystyle \int_0^\infty \frac{u^{-z}}{1+u} \, du = \frac{\pi}{\sin \pi z} \) を示す。積分の存在を示さなければならないが、それは最後にする。\( \displaystyle f(u) = \frac{u^{-z}}{1+u} = \frac{e^{-z \log u }}{1+u} \) は \(u=0\) が分岐点、\( u=-1 \) が極である。例によって右図のような積分路 (外を大きく反時計回り、原点周りを小さく時計回り)をとる。\( 0 < \epsilon < 1 < R \) として、以下の積分路 \(C=L_1+C_R+L_2+C_\epsilon \) をとる。
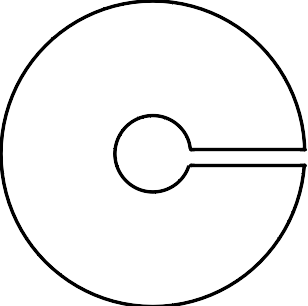
\( \begin{eqnarray}
&& L_1: u = t \quad (t:\epsilon \rightarrow R) \\
&& C_R: u = Re^{it} \quad (t:0 \rightarrow 2\pi) \\
&& L_2: u = t \quad (t: R \rightarrow \epsilon) \\
&& C_\epsilon: u = \epsilon e^{it} \quad (t:2\pi \rightarrow 0) \\
\end{eqnarray} \)
留数定理を用いて積分路 \(C\) 上の積分値を求める。
\( \begin{eqnarray}
\int_C f(u) \,du
&=& 2\pi i \, \mathop{\rm{Res}}\limits_{u=-1} \, \frac{e^{-z \log u }}{1+u} \\
&=& 2\pi i \, e^{-z \log (-1)} \\
&=& 2\pi i \, e^{- \pi i z }
\end{eqnarray} \)
\( L_1 \) と \(L_2\) 上の積分値を計算する。2つの積分路は同じ区間を往復しているだけのように見えるが、分枝が異なるために差が生じる。
\( \begin{eqnarray}
\int_{L_1+L_2} f(u) \,du
&=& \int_\epsilon^R \frac{t^{-z}}{1+t}\,dt \,- \int_\epsilon^R \frac{e^{-z(\log t + 2\pi i)}}{1+t}\,dt\\
&=& \left(1 \,-\, e^{-2\pi i z} \right)\int_\epsilon^R \frac{t^{-z}}{1+t}\,dt\\
\end{eqnarray} \)
以上から次の式が得られる。
\( \begin{eqnarray}
2\pi i \, e^{- \pi i z }
&=& \int_{L_1+L_2} f(u) \,du + \int_{C_R} f(u)\,du + \int_{C_\epsilon} f(u)\,du \\
&=& \left(1 \,-\, e^{-2\pi i z} \right)\int_\epsilon^R \frac{t^{-z}}{1+t}\,dt + \int_{C_R} f(u)\,du + \int_{C_\epsilon} f(u)\,du\\
\end{eqnarray} \)
\( \epsilon \rightarrow +0, \, R \rightarrow \infty \) とした時、最後の式の後2項が 0 に収束することは後で示すとしてとりあえず認めると次式が得られる。
\( \begin{eqnarray}
\int_0^\infty \frac{t^{-z}}{1+t}\,dt
&=& \frac{2\pi i \, e^{- \pi i z } }{1 \,-\, e^{-2\pi i z} } \\
&=& \frac{\pi}{\,\frac{e^{\pi i z } \,-\, e^{-\pi i z}} {2i}\, } \\
&=& \frac{\pi}{\sin \pi z} \\
\end{eqnarray} \)
円周上の積分の評価
証明で後回しにした \( C_R,\, C_\epsilon \) 上の積分値が 0 に収束することを示す。分母の評価に三角不等式 \( |a+b| \geq |a|-|b| \) をしばしば用いる。以下の議論で \( z > 0 \) かつ \( 1-z > 0 \) に注意しておきたい。
\( \begin{eqnarray}
\left| \int_{C_R} f(u)\,du \right|
&=& \left| \int_0^{2\pi} \frac{R^{-z}e^{-izt}}{1+Re^{it}}\,iR e^{it}\,dt \right| \\
&\leq& R^{1-z} \int_0^{2\pi} \frac{1}{\left|1+Re^{it}\right|} \,dt \\
\end{eqnarray} \)
\(R\) が十分大きい時、\(\displaystyle \left|1+Re^{it}\right| > R \,-\, 1 > \frac{R}{2} \) だから
\( \begin{eqnarray}
\left| \int_{C_R} f(u)\,du \right|
&\leq& R^{1-z} \cdot \frac{2}{R} \cdot 2\pi = \frac{4\pi}{R^z} \rightarrow 0 \quad(R\rightarrow \infty ) \\
\end{eqnarray} \)
次に \( C_\epsilon \) 上の積分値を評価する。
\( \begin{eqnarray}
\left| \int_{C_\epsilon} f(u)\,du \right|
&=& \left| \int_0^{2\pi} \frac{\epsilon^{-z}e^{-izt}}{1+\epsilon e^{it}}\,i\epsilon e^{it}\,dt \right| \\
&\leq& \epsilon^{1-z} \int_0^{2\pi} \frac{1}{\left|1+\epsilon e^{it}\right|} \,dt \\
\end{eqnarray} \)
\(\epsilon\) が十分小さい時、\(\displaystyle \left|1+\epsilon e^{it}\right| > 1 \,-\, \epsilon > \frac{1}{2} \) だから
\( \begin{eqnarray}
\left| \int_{C_\epsilon} f(u)\,du \right|
&\leq& 4 \pi \epsilon^{1-z} \rightarrow 0 \quad(\epsilon \rightarrow +0 ) \\
\end{eqnarray} \)
積分の存在
\( 0 < z < 1 \) の下で \( \displaystyle \int_0^\infty \frac{u^{-z}}{1+u} \, du \) の存在を示すために、次の2つの基本的な定理を使う。
(1) \( \quad \alpha < 1 \) ならば \( \displaystyle \int_0^1 \frac{1}{x^\alpha}\,dx \) は収束する。
(2) \( \quad \alpha > 1 \) ならば \( \displaystyle \int_1^\infty \frac{1}{x^\alpha}\,dx \) は収束する。
要は \( \displaystyle \frac{1}{x} \) を境に収束性が変わる。\( \displaystyle \int_0^\infty \frac{u^{-z}}{1+u} \, du = \int_0^1 \frac{u^{-z}}{1+u} \, du + \int_1^\infty \frac{u^{-z}}{1+u} \, du \) と分解して、2つの広義積分が収束することを示す。
1つ目の積分 \( \displaystyle \int_0^1 \frac{u^{-z}}{1+u} \, du \) の存在
\( 0 \leq u \) より \( \displaystyle 0 \leq \frac{u^{-z}}{1+u} \leq \frac{1}{u^z} \) となる。 \( 0 < z < 1 \) だから (1) より収束する。
2つ目の積分 \( \displaystyle \int_1^\infty \frac{u^{-z}}{1+u} \, du \) の存在
\( 1 \leq u \) より \( \displaystyle 1+u > \frac{u}{2} \) だから \( \displaystyle 0 \leq \frac{u^{-z}}{1+u} \leq \frac{2u^{-z}}{u} = \frac{2}{u^{1+z}}\) となる。 \( 1+z > 1 \) だから (2) より収束する。
他の証明法?
\( \Gamma(z) \, \Gamma(1-z)\,\sin \pi z \) が有界な整関数であると示せば Liouville の定理により示せそうに思うが、手持ちのテキストではその方針の証明は見つからなかった。見つかれば追記しておきたい。

