複素関数論で鏡像関係を定義するためにアポロニウスの円を導入する。議論では複素数は使わない。
アポロニウスの円の定義
複素平面上の2点 \( \alpha, \beta \) と実数 \( 0<k<1 \) に対して、\( |z-\alpha| = k|z-\beta| \) を満たす \(z\) の集合は円を成しアポロニウスの円と呼ばれる。\(k\) について制限はついているが、\(k>1\) の場合は \( \frac{1}{k}|z-\alpha| = |z-\beta| \) として、2点の役割が逆転するだけである。\(k=1\) の場合は2点を結ぶ線分の垂直二等分線であり、リーマン球上では無限遠点を通る円であるので、これもアポロニウスの円に含めても良い。複素数を使って定義はしたものの図形的な意味を考えれば複素数を使う必要はなく、初等幾何でも議論しても良い。\(xy\) 平面上でアポロニウスの円を \(\alpha\) が原点になるように平行移動、その後 \( \beta \) が実軸上の正の部分に来るように回転移動させて、\( \alpha, \beta \) の移動先をそれぞれ \( P(0,0),\,Q(a,0)\,(a>0) \) とする。このときアポロニウスの円は \( x^2+y^2 = k \left( (x-a)^2 + y^2 \right) \) となる。これを変形して
\( \begin{eqnarray}
\left( x \,-\, \frac{ak^2}{k^2-1} \right)^2 + y^2 &=& \frac{a^2k^2}{\left( k^2-1 \right)^2 }
\end{eqnarray} \)
となり、中心 \( \left( \frac{ak^2}{k^2-1},0 \right) \)、半径 \( \frac{ak}{1 \,-\, k^2} \) の円と確認できた。中心は実軸上の負の部分にある。
鏡像関係
アポロニウスの円を \(C\) で表し、半径を \(R\) とする。上の議論から \( R=\frac{ak}{1 \,-\, k^2} \) である。\(C\) の中心から点 \( P,Q \) への距離をそれぞれ \( p,q \) とすると、\( p=\frac{ak^2}{1\,-\,k^2},\, q=a+p=\frac{a}{1\,-\,k^2} \) である。この時の \(pq\) を計算してみよう。
\( \begin{eqnarray}
pq &=& \frac{ak^2}{1\,-\,k^2} \cdot \frac{a}{1\,-\,k^2}
\,=\, \frac{a^2k^2}{\left( 1\,-\,k^2 \right)^2} \,=\, R^2
\end{eqnarray} \)
したがって、\(pq\) はアポロニウスの円の半径の二乗に等しい。
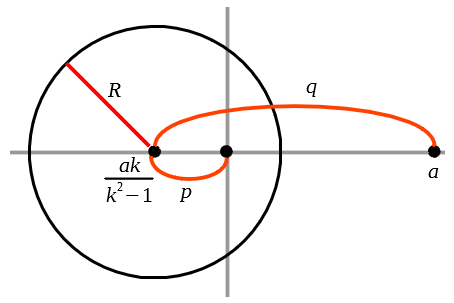
逆に半径 \(R\) の円 \(C\) を与えて、内部の点 \(P\) をとる。\(P\) は \(C\) の中心とは異なる点とし、中心からの距離を \(p\) とする。\(C\) の中心から \(P\) に向けた半直線の上で \(C\) からの距離が \( \frac{R^2}{p} \) の点を \(Q\) とする。点 \(Q\) は唯一つに定まり、\(P\) と \(Q\) は \(C\) に関して鏡像関係にあるという。先に円の外部の点 \(Q\) をとり \(C\) の中心からの距離を \(q\) とした場合も半直線上に \(C\) の中心からの距離が \(\frac{R^2}{q}\) となる点 \(P\) を取った場合も同様である。\(P\) が \(C\) の中心の場合は無限遠点と鏡像の関係にあると定義する。\( P \) を \(C\) の中心に近づけると、\(Q\) は無限遠に向かうので自然な定義である。\(P\) が円周上の場合は、\(P\) 自身と鏡像関係にあり、この場合も \(pq=R^2\) は成り立つ。
鏡像関係からアポロニウスの円
与えられた円 \(C\) に対して鏡像関係にある2点によるアポロニウスの円として表すことができるだろうか。\(C\) の中心を原点、半径を \(R\) とする。鏡像関係にある点の一方は円の内部にあり、必要であれば実軸上の正の部分に回転移動させ、\( (p,0) \,(0<p<R)\) とすると、鏡像関係にある点は \( \left( \frac{R^2}{p},0 \right) \) である。\(C\) 上の点 \( (x,y) \) は \( x^2+y^2=R^2\) を満たす。
\( \begin{eqnarray}
\frac{(x-p)^2+y^2}{\left( x\,-\,\frac{R^2}{p} \right)^2+y^2}
&=& \frac{R^2 -2px + p^2}{R^2 -\frac{2R^2}{p}x+\frac{R^4}{p^2}}
\,=\, \frac{p^2}{R^2} \\[3mm]
\left| (x-p)^2+y^2 \right|
&=& \frac{p}{R} \left| \left( x-\frac{R^2}{p} \right)^2+y^2 \right|
\end{eqnarray} \)
したがって、\(C\) はアポロニウスの円として表され、\(k=\frac{p}{R}\) である。
直線に関する鏡像関係
直線はリーマン球上では無限遠点を通る円だったので、鏡像関係に関する妥当な定義ができそうである。アポロニウスの円の定義で \(k=1\) とすれば直線が得られ、\(P,Q\) は直線について対称である。直線に関する鏡像関係は、直線について対称であることと定義する。この定義の妥当性のためには性質を良く調べる必要がありそうだ。解析接続における実軸に関する対称性の利用は鏡像の原理と呼ばれ、鏡像関係は直線に関する方が良く知られているのかもしれない。

